
 (Note: This is an equal lateral triangle).
(Note: This is an equal lateral triangle).

Introduction:
Computer scientists often use simulation programs to help develop a better understanding of systems or processes that are highly complex and thus are difficult or impossible to analyze theoretically. For example, before actually building the newest CPU, computer scientists and engineers will develop a program that simulates the CPU and use this simulation to verify that the CPU is designed correctly. Similarly, computer scientists have used simulation programs in experiments to test and evaluate new techniques for transmitting information across the internet and between wireless devices such as PDAs and cell phones. In other fields, computer scientists might help to develop simulation programs and experiments involving the evaluation of new medications, understanding the human genome or even testing theories of cognition and evolution. To be effective in these situations computer scientists must have a solid set of empirical skills that assist them in designing and performing experiments as well as in analyzing the results and drawing valid conclusions.
In this lab you will create some small programs that simulate a physical
process known as a random walk. You will then use your simulation
programs to perform experiments, collect and analyze data and draw conclusions
about two different types of random walk. Through this process you will gain
experience with the techniques and issues involved in analyzing the data
obtained from experiments involving computer simulations. But before jumping
into these experiments you will spend a little time learning the programming
language that you will use to write your simulations.
Turtle Graphics:
You will write your simulations in a sub-set of a language called LOGO. The sub-set of LOGO that you will use is called turtle graphics. With turtle graphics, your program consists of a series of commands that move a virtual turtle around on the computer screen. While you will not actually see the turtle on the screen, as your program executes the turtle will leave behind a line on the screen showing the path that it has followed.
To get started click on the following link to launch the Random Walks Application. In the left part of the window is a text area labeled "Turtle Code" in which instructions can be entered for controlling the movement of the turtle. When the button labeled "Run Turtle Code" is clicked, these instructions are executed and the turtle moves accordingly in the "Turtle Visualization" screen on the right. The "Turtle Visualization screen is 30 units wide and 30 units tall. The center of the screen is considered to be coordinate (0,0), so the x-axis (horizontal) ranges from -15 to 15, similarly the y-axis (vertical) also ranges from -15 to 15. When you first open the application, the turtle is located at the center of the screen (0,0) and is facing straight right. You can't see the turtle itself, but you can follow its trail as it moves around on the screen. The coordinates of the turtle, along with its current heading (0 = right, 90 = up, 180 = left, etc.) and distance from the origin, are also displayed in the "Turtle Visualization" screen.
Instructions that can be entered into the "Turtle Code" box to control the turtle include the following:
forward(...): Moves the turtle forward by the number of units
specified in the parenthesis. For example: forward(10) will move
the turtle forward by ten units.
right(...): Rotates the turtle to the right (clockwise) by
the number of degrees specified in the parenthesis. For example:
right(45) rotates the turtle to the right by 45 degrees.
left(...): Rotates the turtle to the left (counter-clockwise)
by the number of degrees specified in the parenthesis.
Note: In programming terms the instructions forward,
left and right are called functions and the
values in the parenthesis are called the arguments to the function.
Exercise 1: Sketch what is drawn by executing each of the following sequences of function calls. Be sure to reset the turtle visualization between each sequence by clicking the button labeled "Clear Turtle Visualization". Note: function calls are executed in order from top to bottom. Also it is perfectly legal to put more than one function call on a line as long as they are separated by a semicolon -- multiple function calls on a single line are evaluated from left-to-right order before moving on to the next line.
You may have noticed that the last sequence of function calls is
repetitive. In particular, it consists of the same two function calls
repeated four times: forward(10); right(90); Instead of repeating
these function calls four times it is possible to enter them only once and
then click on the "Run Turtle Code" button four times without clearing the
turtle visualization between clicks (Try it!). To further simplify the
execution of repeated turtle code, you can enter the number of times to repeat
the code in the text field directly below the "Turtle Code" box. If you enter
a 4 in this box and then click on the "Run Turtle Code" button the effect will
be the same as clicking the "Run Turtle Code" button four times in succession
(Try it!).
Exercise 2: In this exercise you will experiment with repeated execution of function calls:
Exercise 3: Give a sequence of function calls and the number of times they should be repeated to produce the figures shown below. Try to make your sequence of function calls as short as possible.

 (Note: This is an equal lateral triangle).
(Note: This is an equal lateral triangle).

In addition to the function calls that you have been using to move the turtle, LOGO also contains a function call that can be used to generate a random integer in a specified range. This function call is:
randomInt(low,high): Generates a random integer in the range
from low up to but not including high. For
example, the function call randomInt(1,100) will generate a
random number between 1 and 99 inclusive.
Exercise 4: What function call would generate random numbers in the following ranges:
One useful thing that can be done with the randomInt function
is to use it (instead of an explicit number) as an argument to the turtle
movement functions. For example: right(randomInt(0,91)); which
will cause the turtle to turn to the right by a random angle between 0 and 90
degrees. Or forward(randomInt(1,11)); which causes the turtle to
move forward between 1 and 10 units.
Exercise 5: Run the turtle code shown below several times using 25 repetitions for each run. Also be sure to clear the turtle visualization between each run. Describe in a few words what what the turtle's path looks like. Explain in a few sentences why the turtles path looks the way it does.
Random Walks in the Country:
Now that you have a little background in programming turtle graphics you are ready to dive into an exploration of random walks. To get a rough idea of what a random walk is you need only imagine a severely dizzy person stumbling around in the middle of an empty farmer's field. If we assume that each step taken by our dizzy person could be in any direction, the result is a random walk. If we were to draw a picture of a random walk it might appear as shown in figure 1. Notice that each straight line segment in the figure represents one step and that the direction of each step has no relationship to any of the previous steps.

Although our imaginary dizzy person provides a funny mental image, it is worth mentioning that random walks also have many important applications. Most notably, random walks provide microscopic models for physical processes such as diffusion and Brownian Motion. Biologists have found uses for random walks as models for gene mutation and genetic drift. Economists have also found random walks useful in analyzing stock performance.
Exercise 6: Create a turtle program that performs a random walk of 100 steps with each step being 1 unit in length. Hint: Your turtle code should turn randomly to one of 360 possible directions and then take a step forward. Give your turtle code and state how many times it should be repeated.
Exercise 7: Use your random walk program to simulate 5 random walks, each with 100 steps of size 1. For each walk, record the final distance from the starting point. Be sure to clear the turtle visualization between each walk so that each new walk starts at (0,0).
Because of their many applications, physicists and mathematicians have studied random walks quite extensively. One quantity that they have found important in studying random walks is the Root Mean Square (RMS) distance. To find the RMS distance of a set of walks, square the distance of each walk, find the average of those squared distances and then take the square root (i.e. find the square root of the mean of the squares!).
Exercise 8: What is the RMS distance for the walks you performed in Exercise 7? Be sure to present your calculation clearly.
The Accuracy of Experimental Results
Mathematical analysis of random walks has shown that we should expect value of the Root Mean Square (RMS) distance for a random walk to be the square root of the number of steps taken in the walk times the length of each step. So for example, for a walk of 144 steps each of size 3, the expected value of the RMS distance would be the square root of 144 (12) times 3 which is 36. When there is a known or accepted value for the result of an experiment, the accuracy of that experiment can be measured by computing the percent error. The percent error provides a measure of the difference between the result found by the experiment and the accepted value. You may recall that the percent error is calculated as:
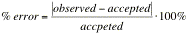
Exercise 9: What is the percent error between the RMS distance of your walks from exercise 8 and the expected value? Be sure to present your calculation clearly.
As you know from your past science classes, if you average the results from many trials, you will tend to get a more accurate result than if you conduct just a single trial. In this case that means that we would expect to get a more accurate result if we average across maybe 20, 50 or 100 runs of the random walk instead of just 5. While this is certainly true, the reasons that it is true are more subtle than you may think. In the next several exercises you will use the Random Walks application to explore why averaging many runs tends to produce an accurate result.
The Random Walk application has several features that will help you with this exploration. The instructions in the rest of this paragraph will start to introduce you to these features. Click on the "Experiment Control" tab in the Random Walks application. This will display a set of controls that allow you to run multiple experiments each of which averages multiple runs of your random walk simulation. Enter a 5 in the "Runs/Exp" field and leave the 1 in the "Experiments" field and click on the "Run Experiments" button. The Random Walk application will run your random walk simulation code 5 times. As each of the 5 random walks is performed you will see it displayed in the "Turtle Visualization" window. When the runs are complete the "Experiment Results" section displays the average, maximum and minimum RMS distance for the experiment that has just been conducted (You can ignore the standard deviation number for now). Note that because you have only run a single experiment, the maximum, minimum and average RMS distances will all have the same value. Click the "Clear Results" button to clear the "Experiment Results" and the "Turtle Visualization".
Exercise 10: In this exercise you will collect data to test the idea that averaging more runs will always produce a more accurate result. To test this idea collect data to complete the table shown below. You do not need to show your calculations. Each row of the table represents an individual experiment so be sure that you have set the "Experiments" field to 1 and be sure to click the "Clear Results" button between each experiment. To make things go more quickly you may collect data for two of the rows of the table yourself and then obtain the data for the other 3 rows from your neighbors. Also, sliding the scroll bar at the bottom of the "Turtle Visualization" to "Fast" will speed things up.
| Experiment | Runs/Exp | |||||
|---|---|---|---|---|---|---|
| 1 | 5 | 20 | ||||
| RMS Dist. | % Error | RMS Dist. | % Error | RMS Dist. | % Error | |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
Exercise 11: Does an experiment that averages more runs always produce a result that is more accurate? Use a specific example from your Exercise 10 data to support your answer.
In all likelihood you answered no to the question in Exercise 11. (If your data did not lead you to answer no, try doing a few more experiments with 1 run each until you get a result that is more accurate than at least one of your 20 run experiments.) So averaging more runs does not guarantee that you will obtain a more accurate result. Rather, by averaging more runs you are only increasing the chances that you will obtain a more accurate result. The next several exercises will help to illustrate this point.
The Consistency of Experimental Results
To better understand why averaging more runs increases your odds for a more accurate result you will look at the distribution of the RMS distances that result when you run multiple experiments. The rest of this paragraph will introduce you to how the Random Walk application keeps track of this distribution. Before beginning, be sure to clear the results of your last experiment. Now set both the "Runs/Exp" and "Experiments" fields to 1 and run the experiment. When the experiment has finished, click on the "RMS Distance Distribution" tab. You should see graph containing a single blue bar. Notice that the location of the bar on the X axis roughly corresponds to the "Average RMS Distance" from the "Experiment Results". Also, notice that the height of the bar is exactly 1.
The graph displayed on the "RMS Distance Distribution" tab is called a histogram. In a histogram the x axis is divided into bins. On the histogram that you are looking at there are 20 bins each of size 1. Each bin can contain a bar and the height of the bar in a bin indicates the number of experiment results the have fallen into that bin. For example, the bin at 12 covers the distances from 12 to 12.999.... So if the RMS Distance of the experiment you performed was 12.59, then the blue bar on the histogram would appear in the bin at 12. Similarly, if the RMS Distance was 4.244 the bar would appear in the bin at 4.
Exercise 12: Click the "Run Experiments" button 20 more times. Be sure not to clear the results between each experiment because clearing the results also clears the histogram. In the experiments you just performed what range of distances (i.e. which bin) occurred most frequently? How can you tell?
If as in Exercise 12 you want to run multiple experiments, instead of clicking repeatedly on the "Run Experiments" button, you can simply enter the number of experiments you want to perform in the "Experiments" box. For example, if you enter 20 in the "Experiments" box and click the "Run Experiments" button, the Random Walk application will run 20 experiments in a row without pausing. The result of each experiment will also be added to the histogram in the "RMS Distance Distribution" window. Try it!
The next several exercises will ask you to analyze data from sets of experiments that average 1, 5 and 20 runs. So before going on, you will need to perform the following sets of experiments:
Note: Saving a distribution does not save it to the disk drive. The distribution is only saved during the current session of the Random Walk application.
Exercise 13: Which set of experiments gave the most consistent results? Which gave the least consistent results? How can you tell just by looking at the distributions which of the three sets of experiments gave the most (least) consistent results?
While looking at the distribution of data as a histogram gives a nice intuitive feel for consistency there are several more formal ways to measure the consistency of a set of data. We'll consider two of those ways here. The simplest way to measure the consistency of a data set is to express the range of the data as a percentage of its mean using the formula:
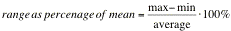
Exercise 14: Record the average, maximum and minimum RMS distances for each of the three sets of experiments you performed above. Compute the range of the data as a percentage of the mean for each set of experiments. Do these measures of consistency agree with your answer from Exercise 13? Be sure to present your computations clearly and use them to justify your answer.
Exercise 15: What do your answers to Exercises 13 and 14 suggest about the relationship between the number of runs averaged in each experiment and the consistency of the results? Be sure to use your data to support your answer.
Standard deviation is another measure of consistency. While the standard deviation is often a better measure of consistency than the range as a percentage of the mean it is also more complex to compute. Thus, what is important here is for you to focus on understanding the meaning of standard deviation instead of how to compute it. You should notice that the standard deviation ("Std. Dev.") is reported on each distribution that you saved in the Random Walks application. The value reported as the standard deviation indicates that most (about 68% percent) of the results fell within one standard deviation of the average. For example, imagine that for a given distribution the average RMS distance is 8 and that the standard deviation is 3. Then for most of the experiments performed, the RMS distance would be between 5 (8-3) and 11 (8+3). In terms of the histogram, most of the area represented by the bars would lie between 5 and 11. This also implies that if you were to conduct another experiment its RMS distance would most likely (about 68/100 times) fall between 5 and 11. Further, if you were to conduct a large number of additional experiments, then about 68% of them would result in RMS distances that fall between 5 and 11.
Exercise 16: Record the standard deviation that is reported on each of your three distributions. According to these standard deviations which set of experiments gave the most consistent results? Which gave the least consistent results? Do these answers agree with those from Exercises 13 and 14?
Exercise 17: As described above the standard deviation requires that most (about 68%) of the data lie within one standard deviation of the mean. When we considered the range as a percentage of the mean we required that all of the data lie within the range. Given this distinction, describe a set of results that would cause your answers to Exercises 14 and 16 to disagree?
Relating Consistency and Accuracy
In the case of the random walk above we knew, thanks to the hard work of some mathematicians, that we should expect the RMS distance to be 10. Because we knew this fact, we could measure the accuracy of our results by calculating the percent error. However, in reality when an experiment is being performed it is quite unusual to know an expected value for the result. Thus, some method other than computing the percent error must be used to evaluate the accuracy of the result. It turns out that (with one caveat) an experiment that produces more consistent results will tend to produce more accurate results. The next several exercises will help to reinforce this point.
Exercise 18: Very often scientists consider a result that is within 10% of an accepted value to be accurate. Using this measure for accuracy, what percentage of the time did you get an accurate result when each experiment consisted of 1 run? 5 runs? 20 runs? HINT: Use your saved distributions and add up the heights of the bars that are within 10% of the expected RMS distance.
Exercise 19: If you were to perform another experiment with either 1, 5, or 20 runs in which case would you be most likely to get an accurate result (within 10% of the expected value)? Use your results from Exercise 18 to explain why.
Exercise 20: What do the last two exercises suggest about the relationship between the number of runs that are averaged in an experiment, the consistency of the results produced by an experiment and the accuracy of the results produced by an experiment?
As mentioned earlier there is a caveat to the general rule you formulated
in Exercise 20. That caveat is that systematic errors in an experiment can
easily produce consistent results that are not accurate. In a physical science
course systematic errors might be caused by a stopwatch that runs a little
slow, a scale that measures a little heavy or a rule that measures a little
short. In experiments involving computer simulations the most common source of
systematic errors are bugs in the simulation program. For example,
imagine that you had made a typo in your random walk program and written the
statement A Random Walk in the City
forward(2) instead of forward(1). Your
program would still have produced consistent results, but they would not have
been accurate for a walk in which each step was supposed to be of size 1.
While this bug would have been quite obvious and unlikely to occur, you can
imagine that as simulation programs become more and more complex it becomes
more and more difficult to recognize and remove the bugs (i.e. systematic
errors).
The random walks that you have been working with so far are called unconstrained walks because the walker may move in any direction at each step. We also called this a random walk in the country because of the analogy using the dizzy person in the farmer's field. Another type of random walk is called a constrained walk. In a constrained walk, the walker can move only in a very limited number of directions at each step. One such walk is often called a city walk. In a city walk, at each step the walker may only go in one of four directions (up, down, left, right). Clearly, the analogy here is a person walking aimlessly around a city making random decisions at each intersection. Figure 2 shows what a typical random city walk might look like.

To program a random city walk in the Random Walks application you will need
to know about one more LOGO function. This function is named
randomOneOf. The randomOneOf function takes a list
of values as an argument and picks one of them at random. For example,
consider the following turtle graphics program:
Each time this turtle code is executed the turtle will turn to the right 30 degrees and then will move forward either 2, 4, 6 or 8 units. Give it a try!
Exercise 21: Create a turtle program that
performs a random city walk of 100 steps with each step being 1 unit in
length. Hint: Your turtle code should turn randomly to one of 4 possible
directions and then take a step forward. Give your turtle code and state how
many times it should be repeated.
An Experiment
At this point a very interesting question to ask would be: How does the the RMS distance of a country walk compare to that of a city walk?
Exercise 22: How would you expect the RMS distance of a country walk to compare to that of a city walk? That is, would you predict that the expected RMS distance for a country walk would be larger, smaller or the same as a city walk with the same number and size of steps? State a hypothesis and a possible rationale for that hypothesis.
To test your hypothesis, perform 50 experiments, each of which averages 20 runs of your city walk simulation. When these experiments are complete, save the distribution so that the results can be compared to those from the corresponding country walk.
Exercise 23: Record the average RMS distance and the standard deviation from your city walk experiment. Comparing these results to those from the corresponding country walk experiment, which type of walk has the larger average RMS distance?
Exercise 24: If you were to perform one country walk experiment that averages 20 walks and then one similar city walk experiment, over and over again, do you think that one type of walk would consistently have a larger RMS distance than the other? Why? Hint: Think about the distributions - what are the odds that an individual country walk experiment has a larger RMS distance than an individual city walk experiment?
Exercise 25: Do you think that comparing the average RMS distance values is sufficient to draw a conclusion about which type of walk has a larger or smaller expected RMS distance? Explain why or why not?
You probably realized in the last few exercises that simply comparing the average RMS distances of the two types of walks is not sufficient. To draw a valid conclusion it is also necessary to consider the distribution of the data. From the earlier exercises you know that if you repeat your experiment many times most of the results (about 68% of them) will lie within one standard deviation of the mean. It turns out that it is also true that nearly every result (about 95% of them) will lie within two standard deviations of the mean. Because of this, it is commonly said that any value within two standard deviations of the mean is a plausible result for the experiment. Conversely, you are very unlikely to see a result that lies more than two standard deviations from the mean.
Exercise 26: What is the range of plausible values for your city walk experiment? (I.e. what is the range of values that lie within two standard deviations of the mean?) What is the range of plausible values for your country walk experiment?
Exercise 27: Is the average RMS distance from your city walk experiment a plausible value for your country walk experiment? Is the average RMS distance from your country walk experiment a plausible value for your city walk experiment?
Exercise 28: Use your answer from Exercise 27 to argue that it is plausible that the expected RMS distance for a city walk is the same as the expected RMS distance for a country walk.
Exercise 29: Imagine that in Exercise 27, you found that the average RMS distance for a country walk was not a plausible value for your city walk experiment and vice versa. What would you conclude about the expected RMS distances of the two types of walks under these conditions? Why?
Note that what you have done in these last few exercises is similar to what statisticians call hypothesis testing. What you have done is quite informal compared to what you might study in a statistics class. However, the ideas you have seen are the same as those that form the basis for formal statistics tools such as the t-test that is used hypothesis testing. If you take a formal statistics course you will study how and when to use a t-test for testing hypotheses such as the one you made in this lab. It is also possible that you might use a t-test in experiments that you perform in your more advanced computer science courses.